Total Internal Reflection – Learn

When light passes from one medium into a less dense medium the ray of light refracts away from the normal and toward the boundary surface. As the angle of incidence increases the refracted angle approaches 90º. If the angle of incidence continues to increase, eventually an angle is reached where the refracted ray will refract at 90º and pass directly along the boundary surface. This angle is known as the critical angle, ic. If the angle of incidence is greater than the critical angle then the light ray will reflect off the boundary surface and obey the law of reflection. When this happens we observe total internal reflection.

For a light ray moving from medium x, (with a refractive index, { n }_{ x }) moving into air, the critical angle { i }_{ c } is given by:

\sin { { i }_{ c } } =\cfrac { 1 }{ { n }_{ x } }

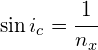
Example 1:

Calculate the critical angle for a light ray passing into water (n=1.33):

Using: 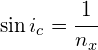\sin { { i }_{ c } } =\cfrac { 1 }{ { n }_{ x } }

\sin { { i }_{ c } } =\cfrac { 1 }{ 1.33 }

\sin { { i }_{ c } } =0.752

{ i }_{ c }=\sin ^{ -1 }{ 0.752 }

{ i }_{ c }=48.75^{ \circ }

Example 2:

A light ray travels from air into a 2nd medium. The critical angle is found to be 56º. Determine the refractive index of the second medium:

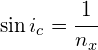
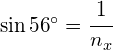
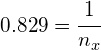
Using: \sin { { i }_{ c } } =\cfrac { 1 }{ { n }_{ x } }

\sin { 56 } ^{ \circ }=\cfrac { 1 }{ { n }_{ x } }

0.829=\cfrac { 1 }{ { n }_{ x } }

{ n }_{ x }=\cfrac { 1 }{ 0.829 }

{ n }_{ x }=1.21