The Wave Equation – Learn
The wave equation relates the velocity, frequency and wavelength of a wave. It can also be useful to incorporate the relationship between the period of a wave and its frequency.
Period and frequency: The period of a wave is inversely proportional to its frequency.
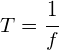T=\cfrac { 1 }{ f } and f=\cfrac { 1 }{ T }
Where:
T = period of the wave in s (seconds)
f = frequency of the wave in Hz (Hertz)
Velocity, frequency, period and wavelength: The relationship between velocity, frequency, period and wavelength is represented by the following:
v=f\lambda and v=\cfrac { \lambda }{ T }
Where:
v = velocity of the wave in { m }/{ s }
\lambda = wavelength in m (metres)
T = period of the wave in s (seconds)
f = frequency of the wave in Hz (Hertz)
Example 1:
What is the velocity of a wave with a wavelength of 2.0 m and a frequency of 10 Hz?
\lambda =2.0
f =10
v=f\lambda
v=10\times 2
v=20{ m }/{ s }
Some questions will require the wave equation to be rearranged:
Example 2:
What is the frequency of a wave with a wavelength of 0.05 m and a velocity of 25{ m }/{ s } ?
\lambda =0.005
v =25
v=f\lambda, rearranged to give: f=\cfrac { v }{ \lambda }
f=\cfrac { 25 }{ 0.05 }
f=500Hz
Some questions will require the units to be changed:
Example 3:
What is the velocity of a wave with a wavelength of 740 nm and a frequency of 400 kHz?
\lambda =740nm = 740\times { 10 }^{ -9 }
f =400kHz = 400\times { 10 }^{ 3 }
v=f\lambda
v=(740\times { 10 }^{ -9 })\times (400\times { 10 }^{ 3 })
v=0.296{ m }/{ s }
Example 4:
What is the period of a wave with a frequency of 2.5 kHz?
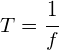
f =2.5kHz = 2.5\times { 10 }^{ 3 }
T=\cfrac { 1 }{ f }
T=\cfrac { 1 }{ 2500 }
T=0.0004s