Acceleration

Acceleration occurs when there is a change in speed – speeding up or slowing down. It is commonly termed acceleration when the speed is increased and deceleration when the speed is decreased. Acceleration can also be described as a change in direction. You may have seen graphs or diagrams illustrating acceleration – velocity-time graphs and ticker-timers:

Acceleration is a vector so is often described as being positive in one direction and negative in the other. Acceleration is defined as a change in velocity divided by the time interval. The equation for acceleration is:

\overset { \rightarrow }{ a } =\cfrac { \Delta \overset { \rightarrow }{ v } }{ t }

\overset { \rightarrow }{ a } =\cfrac { \overset { \rightarrow }{ v } -\overset { \rightarrow }{ u } }{ t }

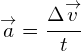
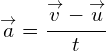
where:

\overset { \rightarrow }{ a } = the acceleration in m/s2

\overset { \rightarrow }{ v } = the final velocity in m/s

\overset { \rightarrow }{ u }  = the initial velocity in m/s

t = the time in s

The equation can be rearranged to calculate any of the variables required.

Example 1:

What is the acceleration of a vehicle that has an initial speed of 3 m/s and it increases its speed to 11 m/s over a time interval of 4 seconds?

using:

\overset { \rightarrow }{ a } =\cfrac { \overset { \rightarrow }{ v } -\overset { \rightarrow }{ u } }{ t }

\overset { \rightarrow }{ a } =\cfrac { 11-3 }{ 4 }

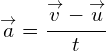
\overset { \rightarrow }{ a } = 2 m/s2

Example 2:

How long does it take a cyclist to accelerate from rest to 4.5 m/s if they are accelerating at 0.5 m/s?

using: 

\overset { \rightarrow }{ a } =\cfrac { \overset { \rightarrow }{ v } -\overset { \rightarrow }{ u } }{ t }

0.5=\cfrac { 4.5-0 }{ t }

t=\cfrac { 4.5 }{ 0.5 }

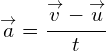
t = 9 s