Radioactive Decay – Learn
Radioactive decay
Around the turn of the 20th century, the scientific world was buzzing with the study of radioactivity. Famously, Henri Becquerel had just discovered strange radiation emitted by a rock sample containing uranium salts, when it had been left in a draw with a photographic plate. Subsequent investigation by prominent scientists of the time included Marie Curie and Ernest Rutherford. Curie, the first female recipient of the Nobel Prize (and only woman to win it twice), discovered new radioactive elements, while Rutherford examined the nature of the radiation in greater detail. Through Rutherford’s work, three different types of radiation where uncovered, each with their own specific properties and conditions for release. These new varieties of radiation were named, alpha, beta and gamma.
Before jumping into greater depth regarding these types of radiation, there is some important terminology that needs to be considered.
Mass number – This refers to the total number nucleons (protons and neutrons) in a specific nucleus.
Atomic number – The amount of protons present in a nucleus, consequently determining the properties of the particular atom. For example, an atom with 8 protons in the nucleus will always be oxygen and an atom with 26 protons in the nucleus will always be iron. There are no exemptions to this.
Isotope – While each element has a specific number of protons in the nucleus, the number of the neutrons can fluctuate. This does not impact the chemical properties of the element, but can change the stability. For example, the nucleus of most carbon atom (98.9%) contain 6 protons and 6 neutrons, however, some carbon nuclei can contain 7 neutrons (1.1%) and other 8 neutrons (only trace amounts, although very important for carbon dating). Each of these isotopes of carbon behaves chemically in the exact same way, although have differing nuclear pathways. All elements are technically isotopes.
Atomic mass – The mass of a specific isotope, not the value found on the period table. This value is generally given in atomic mass units (u), a conversion to kg can be found in the data sheet (1 u = 1.661 x 10-27 kg). Should quantitative analysis of a nuclear reaction be required, this is the value that needs to be used.
Atomic weight – This is the value found in the period table. It is a relative atomic mass considered all isotopes of the element and their relative abundances. It should not be used in quantitative analysis.
Stability – The likelihood of a nucleus to undergo nuclear decay. A stable isotope will never decay, however, an unstable element will decay at some point. An example of a stable element is helium-4 (the isotope of helium with 2 protons and 2 neutrons), on the otherhand, an element like polonium has no stable isotopes.
Radioactive decay – A natural and spontaneous process which involves the emission of radiation from an unstable nucleus.
Transmutation – When the number of protons is changed in a nucleus through a nuclear reaction, thus forming a different element.
The figure above shows how different isotopes can be presented in equations. On the left is a general format, with X representing the chemical symbol of an element, A representing the mass number and Z the number of protons. Using this system, the isotope in the middle can be identified as hydrogen with one proton and no neutrons (given that the sum of the nucleons is also one). The isotope on the right is fluorine, containing 9 protons and 10 neutrons (as the total number of nucleons is 19). When writing isotopes in a sentences, just the chemical name or symbol and the mass number is recorded. For example, chlorine-35 (Cl-35), uranium 238 (U-238), and strontium-88 (Sr-88).
Alpha decay
Alpha decay occurs when the nucleus is simply too big, straining against the forces that keep it bound together. It involves the emission of an alpha particle, which is identical to a helium-4 nucleus, from the nucleus of an unstable atom. It has the same atomic mass as helium-4 and a positive net charge, containing 2 protons and no electrons, the magnitude of this charge can be determined using the charge of an electron from the data sheet (remember, the charge of a proton is equal in magnitude to the charge of an electron). As the result of alpha decay, the number of protons and neutrons present in the daughter nuclei (after the release of the alpha particle) has changed, thus a transmutation has occurred and a new element formed. Due to the relatively large size of alpha particles, compared to other types of radiation, they are easily stopped by materials. A piece of paper between the radioactive source and a Geiger counter (a measuring tool for radiation), is enough to bring the count to zero.
The general equation for an alpha decay has been provided below, showing the number of nucleons decreasing by 4, the atomic number decreasing by 2, and the emission of the alpha particle. The initial element is known as the parent nuclei, and the decayed nuclei, the daughter nuclei.
Beta decay
There are two varieties of beta decay which can occur, beta positive and beta negative decay. Both occur when the ratio of protons to neutrons in the nucleus leads to instability. In beta negative, there are too many neutrons in the nucleus relative to the number of protons, and in beta positive, there are too many neutrons relative to the number of protons. In general, beta decay is more penetrative than alpha decay, and takes several millimetres of lead to obstruct (or larger amount of a less dense material).
Beta negative decay
In beta negative decay, one of the overabundant neutrons in the nucleus will turn itself into a proton, emitting a beta particle (which is identical to an electron in terms of mass and charge) and an antineutrino. The term neutrino may be unfamiliar, for now it is enough to know that they are extremely small fundamental particles that rarely interact with matter. An antineutrino is the antimatter counterpart of this particle. When beta negative decay occurs, the number of protons in the nucleus increases, meaning that a new element has been formed. The general formula for this nuclear reaction has been outlined below.
In this equation the notation for an electron and an antineutrino can be seen. Due to the mass of an electron being orders of magnitude smaller than the other subatomic particles, their masses are largely ignored in nuclear reactions. It is given an atomic number of -1, so that the atomic numbers on both sides of equation remain balanced. All antimatter particles are represented using the same symbol as the corresponding matter particle, but with a bar above the symbol. Antineutrinos, and neutrinos, are extremely small and uncharged, hence do not contribute to mass number or atomic number.
Beta positive decay
Beta positive decay is very similar to beta negative decay, achieving the opposite outcome, turning a proton into a neutron. In order for this to occur, the neutron will emit a positron (the antimatter counterpart of the electron) and a neutrino. Consequently, the general formula looks very similar.
As can be seem in this nuclear equation, the atomic number decreases in this reaction, while the mass number, similarly, stays constant. It is important to note, that a general reference to beta decay in the HSC course tends to focus on beta negative decay, approach questions with this in mind.
Gamma decay
Gamma decay was the last type of radiation to be identified, as unlike alpha and beta decay it is the emission of a photon from the nucleus instead of a particle. There are two circumstances where gamma decay occurs, through the release of energy from an “excited” nucleus, or as a byproduct of another nuclear reaction. Gamma radiation is an extremely high energy photon of electromagnetic radiation, generally only produced in nuclear reactions. As a result of this, it has great penetrating power and is capable of passing through up to a metre of concrete, much greater than either alpha or beta radiation. As electromagnetic radiation does not have a charge or mass, a transmutation does not occur. This be observed in the general formula below.
There is another new symbol in this formula, which may require some explanation. The lowercase m next to the mass number recognises that this isotope is metastable, indicating that the nucleus is currently arranged in an excited state. This represents the energy that is released during gamma decay. For example, technetium-99m decays via gamma decay to form technetium 99 with a photon of gamma radiation emitted, the detection of this gamma radiation is an important diagnostic technique in cancer treatment.
Half life and exponential decay graphs
While radioactive decay is a random, natural process, the stability of an atom influences how quickly this decay is likely to occur. As a minute amount of a material contains millions upon millions of atoms, the rate of decay can accurately be predicted due to the huge sample size. The most common means of measuring the decay of an element is through examining it’s half life. The half life of an isotope is the point at which half an original sample (an amount of atoms or a mass) remains, and this can range from fractions of a second to billions of year. What is important to remember is that when an element has decayed, it has not disappeared, it has simply decayed into a different element. For example, when investigating the decay of uranium-238, which naturally undergoes alpha decay, that when 75% of an initial sample remains, the other 25% has already decayed to thorium-234.
Radioactive decay is exponential, and this is a useful term to understand. It means that after each time period observed that only a percentage of the amount remains, which is very different to a linear decrease, which would mean that a constant amount is subtracted each time. To assist with understanding the difference, and exemplify the characteristic shape of a decay, see the comparison below.
The x-axis represents time, and the y-axis represents the number of an initial amount remaining. Each graph starts with the loss of 10% of the total initial amount, though this is constant for the linear decay and dependent on the amount remaining for the exponential decay. As a result of this, there is none of the initial amount remaining after ten decay periods on the left, however, after 50 decay periods some proportion of the initial amount remains on the right.
It is possible to determine the half life of an element graphically, and sometimes this is required for further analysis. Consider the decay curve of the unknown element in the graph below. It can be seen that initially there are 1000 atoms of the unknown element, which decreases by a consistent proportion every decay period (which could be measured in seconds, hours, days or years). To determine the half life of this element, the time must be found when 500 atoms remain, half of the initial sample. Graphically, this can be determined to be 4 decay periods. It is important to note that after 8 decay periods 250 atoms remain and after 12 decay periods 125, a consistent halving of the atoms remaining every 4 decay periods.
The decay equation
For deeper analysis, the use of the decay formula is required. It provides greater specificity and can be applied to make accurate predictions.
![]()
Where:
N0– The initial number of atoms (or mass of sample).
Nt – The amount of atoms remaining after time t.
λ – The decay constant, the rate at which this specific isotope decays (this is unique for all isotopes).
t – The number of time periods (this formula does not contain units of time, and will work with any units of time provided that they are consistent).
The decay formula can be rearranged to find the decay constant for an isotope, should the half life be provided. It is good to be able to understand the derivation, but the final expression is provided in the data sheet.
![]()
![]()
![]()
![]()
![]()
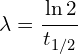
Example 1:
Predict the products of the alpha decay of Radium-222.
Answer:
Radium-222 contains 222 nucleons, 88 of which are protons (this can be ascertained from the periodic table in an exam). When it undergoes alpha decay, an alpha particle is emitted with 2 protons and 2 neutrons, this is one of the products. As a consequence of this emission, the mass number of the other product must decrease by four and the atomic number by two. Therefore, this daughter nuclei has 218 nucleons, including 86 protons. All elements with 86 protons are radon (periodic table), hence the isotope radon-218 has been formed.
The products of this alpha decay are an alpha particle (helium-4) and radon-218.
Example 2:
Predict the products of the beta negative decay of carbon-14.
Answer:
The nucleus of a carbon-14 atom contains 6 protons and 8 neutrons, determined through considering the atomic number and mass number of the isotope.Through beta negative decay, one of the neutrons will turn into a proton, releasing an electron and an antineutrino. This means that the nucleus will now contain 7 protons and 7 neutrons, thus nitrogen-14 has been formed.
The products of this beta negative decay are nitrogen-14, an electron and an antineutrino.
Example 3:
Predict the products of the beta positive decay of sodium-22.
Answer:
The nucleus of a sodium-22 atom contains 11 protons and 11 neutrons, determined through considering the atomic number and mass number of the isotope. Through beta positive decay, one of the protons will turn into a neutron, releasing a positron and a neutrino. This means that the nucleus will now contain 10 protons and 12 neutrons, thus neon-22 has been formed.
The products of this beat positive decay are neon-22, a positron and a neutrino.
Example 4:
Iodine-131 has a decay constant of 0.086 per day. If a sample of rock contains 10 g of iodine-133, determine the amount remaining after three weeks.
Answer:
![]()
![]()
![]()
Following three weeks (21 days), 1.64 g of iodine-133 will remain.
Example 5:
Argon-42 has a half-life of 33 years. Determine what proportion of a sample of argon-42 would remain after 75 years.
Answer:
Step 1 – determine decay constant
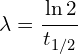
![]()
![]()
Step 2 – determine proportion remaining
![]()
![]()
![]()
21% of the argon-33 would remain.
