Transformers – Learn
A transformer is a device that can increase or decrease AC voltages. They are found in many electrical devices (television sets, radios, battery chargers, phones and electronic keyboards). They are also an essential component of any electrical distribution network. They are used to step up or step down voltages in order to reduce power loss during electrical energy distribution.
Most appliances in the home use transformers to convert the standard residential 240V into smaller voltages which are suitable for devices:
Structure and Function of a Transformer
Transformers consist of two coils of insulated wire called the primary and secondary coils. These coils need to be placed near each other so that an AC current can flow through the primary coil and induce a current in the secondary coil. They can be wound together onto the same soft iron core, or linked by a soft iron core.
AC current is used as this produces a changing magnetic flux in the primary coil. This changing field is needed to induce a current in the secondary coil. If DC current was used there would be no changing magnetic flux, hence, no current induced in the secondary coil.
Transformers are designed so that nearly all of the magnetic flux produced in the primary coil passes through the secondary coil. In an ideal transformer, 100% energy efficiency is assumed for the purposes of calculations in problems. However, in reality, not all of the magnetic flux may pass through the secondary coil and there are other sources of resistance, or energy loss. These will be explored in the next section.
The Transformer Equation
The voltage that is input into a transformer is connected to the primary coil. The voltage that is produced in the secondary coil will be dependent on the number of turns in the secondary coil. However, the frequency of the AC current that is produced will be the same as the primary coil.
Although most transformers are very efficient (99% efficiency), problems that you see will mostly assume ideal transformer conditions, ie: 100% efficiency. The transformer equation that relates the voltage and the number of turns in each coil is:
![]()
where:
![]() is the voltage supplied to the primary coil (in V)
is the voltage supplied to the primary coil (in V)
![]() is the voltage produced in the secondary coil (in V)
is the voltage produced in the secondary coil (in V)
![]() is the number of turns in the primary coil
is the number of turns in the primary coil
![]() is the number of turns in the secondary coil
is the number of turns in the secondary coil
Step-up and Step-down Transformers
A step-up transformer will produce a higher voltage in the secondary coil and the number of turns in the secondary coil will be higher than in the primary coil.
A step-down transformer will produce a lower voltage in the secondary coil and the number of turns in the secondary coil will be lower than in the primary coil.
Transformers and Power
Ideal transformers follow the Law of Energy Conservation. This means that the power input to the primary coil is equal to the power output from the secondary coil. Since ![]() :
:
![]()
![]()
where:
![]() is the voltage supplied to the primary coil (in V)
is the voltage supplied to the primary coil (in V)
![]() is the voltage produced in the secondary coil (in V)
is the voltage produced in the secondary coil (in V)
![]() is the current in the primary coil (in A)
is the current in the primary coil (in A)
![]() is the current in the secondary coil (in A)
is the current in the secondary coil (in A)
Further equations can now be derived given the above relationships. For example:
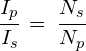
Transformer equations combined:
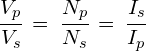
Example:
The transformer in a phone charger reduces a 240V AC voltage to a 6.0V AC voltage. If the secondary coil has 20 turns and the phone draws a current of 200 mA, calculate the following:
a) the number of turns in the primary coil
b) the current in the primary coil
c) the power output of the transformer.
Answers:
a) using: ![]()
![]()
![]()
![]() turns
turns
b) using: 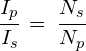
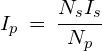
![]()
![]() A = 5mA
A = 5mA
c) using: ![]()
![]()
![]() W
W
