Electromagnetic Induction - Learn

Electromagnetic Induction – Learn

Electromagnetic induction is made use of in motors and transformers which will be explored later. This section will cover both Faraday’s Law of Induction and Lenz’s Law. These laws are important in understanding electromagnetic induction.

Faraday conducted many investigations with magnetic fields and coils of wire. In one investigation he discovered the following:

if he was to move a magnet into the coil it would induce an emf which resulted in a current in the coil
when the magnet was removed, the same current could be observed but in the opposite direction
the faster the motion of the magnet into the coil, the larger the current
if the magnet was held still and the coil moved to create the same relative motion, the observations above were all still observed

Faraday concluded that it did not matter whether it was the magnet or the coil which moved, it was a change in flux that induced an emf, resulting in any observed current. Further to this, he discovered it was the rate of change of flux that determined the magnitude of any emf or current.

Faraday’s Law of Induction

Faraday’s Law of Induction states that: The induced emf in a circuit is equal in magnitude to the rate at which the magnetic flux through the circuit is changing with time.

Faraday’s law can be written in equation form as:

$\varepsilon \:=\:-N\cfrac { \Delta \phi }{ \Delta t }$

where:

$\varepsilon$ is the induced emf (in V)

$N$ is the number of turns in a coil

$\Delta \phi$ is the magnetic flux (in Wb)

$\Delta t$ is the change in time (in s)

*note: the negative sign in the equation tells us the direction of the induced emf which will be discussed later.

Lenz’s Law

Lenz’s law is used to determine the direction of an induced current as a result of an induced emf. It also demonstrates how electromagnetic induction follows the law of conservation of energy.

Lenz discovered a way to predict the direction that a current will flow as result of a changing magnetic field around a conductor (wire, coil, solenoid).

Lenz’s law can be stated as: An induced emf always gives rise to a current that creates a magnetic field that opposes the original change in flux through the circuit.

Recall the negative sign in the equation. This is referencing the idea that the induced current creates a field which is opposite to the original field.

When applying Lenz’s law, there are three steps that can be used to assist in determining the direction of an induced current:

In which direction is the magnetic field changing?
In which direction will a magnetic field oppose this field?
In which direction must the induced current flow to create this field?

Solenoids and Electromagnetic Induction

Recall that a solenoid is a coil of conducting wire that produces a magnetic field when it has a current running through it. Solenoids can also be used to induce currents in other solenoids. They also have the advantage of not requiring moving parts. Rather, they use changes in current to produce a changing magnetic flux. The diagram below illustrates a typical setup that could be used to demonstrate electromagnetic induction using solenoids:

The following animation can be used to demonstrate electromagnetic induction. Observe the differences in the induced current when moving the magnet at different speeds, changing the polarity of the magnets and also using different coils.

Example 1:

Use Lenz’s law to determine the direction of the induced current in each of the examples below:

Answers: (following the 3 steps outlined above)

a) The direction of the magnetic field is increasing and downward through the coil. A magnetic field directed upward through the coil will oppose this change. Using the right hand grip rule, with fingers up through the coil indicates the current flows anticlockwise viewed from above.

b) The direction of the magnetic field is decreasing and upward through the coil. A magnetic field directed upward through the coil will oppose this change. Using the right hand grip rule, with fingers up through the coil indicates the current flows anticlockwise viewed from above.

c) The direction of the magnetic field is increasing into the coil/page. A magnetic field directed outward through the coil/page will oppose this change. Using the right hand grip rule, with fingers out through the coil indicates the current flows anticlockwise.

d) The direction of the magnetic field is decreasing out of the coil/page. A magnetic field directed outward through the coil/page will oppose this change. Using the right hand grip rule, with fingers out through the coil indicates the current flows anticlockwise.

Example 2:

The diagram below illustrates a rectangular loop moving into a magnetic field with a strength of 0.5T into the page over a 0.1s time interval. Determine the following:

a) The magnitude of the emf induced in the loop?

b) Which direction does the current flow around the loop?

Answers:

a) using: $\varepsilon \:=\:-N\cfrac { \Delta \phi }{ \Delta t }$

where:

$N=1$

$\Delta \phi \: =\: { \phi }_{ f }-{ \phi }_{ i }\: =\: ((0.5\times 0.015\times 0.008)\: -\: (0\times 0.015\times 0.008))\: =\: \: 6\times { 10 }^{ -5 }\: T$ *

*note: $\phi =BA$ and the field is parallel to the normal to the area of the coil.

$\Delta t\:=\:0.1s$

$\varepsilon \: =\: \cfrac { 6\times { 10 }^{ -5 } }{ 0.1 } \:=\:6\times { 10 }^{ -4}\:V$

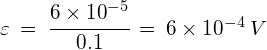
b) The direction of the magnetic field is increasing out of the coil/page. A magnetic field directed inward through the coil/page will oppose this change. Using the right hand grip rule, with fingers out through the coil indicates the current flows clockwise.