Charges in Electric Fields - Learn

Charges in Electric Fields – Learn

An electric field exists around charged particles and objects. The electric field will exert a force on other charged objects. The force experienced can be an attractive or repulsive force depending on the types of charges interacting. The direction of the electric field is the direction that a positive test charge would experience a force when placed in that field.

Uniform Electric Fields

Uniform electric fields exist between charged plates. If positive and negative charged plates are setup facing each other, the lines of electric field in the space between the plates would be evenly spaced. The magnitude of the strength of the field would be constant. This is called a uniform electric field.

A charge that is placed in a uniform electric field would experience a constant electric force:

$\overset { \rightarrow }{ F } =q\overset { \rightarrow }{ E }$

Where:

$\overset { \rightarrow }{ F }$ is the force on the charged particle (N)

$q$ is the charge on the object experiencing the force (C)

$\overset { \rightarrow }{ E }$ is the strength of the electric field in NC⁻¹

The direction of the force on a positive charge will be in the direction of the field, and the force on a negative charge will be opposite to the field direction. Because the force acting on the charge is constant, the acceleration of that charged particle will be constant within the uniform electric field, as given by the equation $F = ma$ .

Electric Field Strength in a Uniform Electric Field

The diagram below demonstrates the electric field between two charged plates, separated by a distance, d.

There is a potential difference between the plates, V, caused by the one plate having a higher potential and the other plate having a lower potential. The strength of the electric field is given by:

$E=\cfrac { V }{ d }$

Where:

$E$ is the electric field strength (Vm⁻¹)

$V$ is the potential difference (V)

$d$ is the distance between the plates (m)

Work Done in Uniform Electric Fields

Work is equal to the change in kinetic energy of a particle or object. Within an electric field, work must be done to move a point charge through the electric field. The source of this work can either be done:

by the electric field on the charged object, or
on the electric field by forcing the object to move

If the charge is moving in the direction that it would naturally be moved by the field then work is being done by the field. If it is moving against the direction it would naturally go then work is done on the field.

To calculate the work done on a point charge to move it through a distance, d, across a potential difference:

$W=qEd$

Where:

$W$ = the work done on the point charge or on the field (in J)

$q$ = the charge of the point charge (in C)

$E$ = the electric field strength (in Vm⁻¹ or NC⁻¹)

$d$ = the distance between the points parallel to the field (in m)

Combining the two equations above, we can derive another equation for work done:

$W=qV$

Where:

$W$ = the work done on the point charge or on the field (in J)

$q$ = the charge of the point charge (in C)

$V$ is the potential difference (V)

Work and Kinetic Energy

As work is equal to the change in kinetic energy, the velocity of a particle can also be determined after calculating the work done by the electric field.

$W=\Delta KE$ and $KE=\cfrac { 1 }{ 2 } m{ v }^{ 2 }$

Comparing Electric and Gravitational Fields

Masses in Gravitational Fields

A mass placed at a point in a gravitational field will experience a force: F = mg.
The mass will accelerate uniformly along the field (parallel to the field lines and in the direction the field lines are pointing) in accordance with Newton’s Second Law. Therefore, $a=\cfrac { F }{ m }$

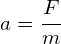
A mass travelling perpendicular to a gravitational field will experience a parabolic trajectory. This is because the only force acting is directed along the field lines.
Its motion has two components: 1. Uniform velocity across the field, and 2. Uniform acceleration along the field.
The combination of these two components produces the parabolic trajectory of a projectile.

Charges in Electric Fields

A charge with mass placed at a point in an electric field will experience a force: F = qE.
As a result, the charge will accelerate uniformly along the field, also in accordance with Newton’s Second Law, hence, $a=\cfrac { F }{ m }$

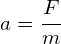
A positive charge travelling with velocity across an electric field will experience a parabolic trajectory. This is because the only force acting is directed along the field lines.
Its motion has two components: 1. Uniform velocity across the field 2. Uniform acceleration along the field.
The combination of these two components produces a parabolic trajectory very similar to projectile motion.

As the trajectory of a charged particle in an electric field resembles that of a projectile and its properties, motion equations can be applied to these problems also.

Example 1:

What acceleration would an electron experience if it was travelling in an electric field of strength 1.5 × 10⁻⁵ NC⁻¹? (q_e = -1.602 × 10⁻¹⁹ C and m_e = 9.109 × 10⁻³¹ kg)

Answer:

Using: $F=qE$

$F=(-1.602\: \times \: { 10 }^{ -19 })(1.5\: \times \: { 10 }^{ -5 })$

$F\:=\:2.403\: \times \: { 10 }^{ -24 }\:N$ (against the electric field)

Extending to Newton’s 2nd Law:

$F\: =\: ma$ and $a\:=\cfrac { F }{ m }$

$a\: =\cfrac { 2.403\: \times \: { 10 }^{ -24 } }{ 9.109\:\times \:{ 10 }^{ -31 } }$

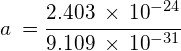
$a\: =\: 2.64\times { 10 }^{ 6 }\: { m }/{ { s }^{ 2 } }$ (in the opposite direction to the electric field)

Example 2:

What is the strength of an electric field between charged plates separated by a distance of 2cm and a potential of 6V across the plates?

Answer:

using: $\vec { E } =\cfrac { V }{ \vec { d } }$

$\vec { E } =\cfrac { 6 }{ 0.02 }$

$\vec { E } =300\: V{ m }^{ -1 }$

Example 3:

a) Calculate the work done on an electron that moves 4cm between charged plates with an electric field strength of 20Vm⁻¹: ${ { (q }_{ e }={ -1.602\times 10 }^{ -19 }C) }$