Electrostatic Force and Electric Fields – Learn
Electric field strength allows us to quantitatively look at electric fields. Mathematically, the electric field, ![]() , is given by:
, is given by:
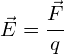
where;
![]() = the electric field strength in
= the electric field strength in ![]()
![]() = the force on the charged particle in
= the force on the charged particle in ![]()
![]() = the charge on the object experiencing the force in
= the charge on the object experiencing the force in ![]()
The previous equation is also commonly arranged to give:
![]()
The acceleration of a charged particle in an electric field can also be determined by using Newton’s 2nd Law:
![]()
where;
![]() = the acceleration of the charged particle in
= the acceleration of the charged particle in ![]()
![]() = the mass of the accelerating particle in
= the mass of the accelerating particle in ![]()
Coulomb’s Law
Coulomb’s Law is used to determine the force between two charged particles:
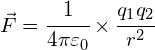
where:
![]() = the force on each charged object (in N)
= the force on each charged object (in N)
![]() and
and ![]() = the charges on the two points (in C)
= the charges on the two points (in C)
![]() = the distance between each charged point (in m)
= the distance between each charged point (in m)
![]() = the permittivity of free space, which is equal to 8.854 × 10−12 A2S4Kg−1m−3 in air or in a vacuum.
= the permittivity of free space, which is equal to 8.854 × 10−12 A2S4Kg−1m−3 in air or in a vacuum.
![]() is known as Coulomb’s constant, k, and is equal to 8.9875 × 109 Nm2C−2. This is usually rounded off to 9.0 × 109 Nm2C−2 for calculations.
is known as Coulomb’s constant, k, and is equal to 8.9875 × 109 Nm2C−2. This is usually rounded off to 9.0 × 109 Nm2C−2 for calculations.
Coulomb’s Law can now become:
![]()
where k = 9.0 × 109 Nm2C−2
Example 1:
Calculate the uniform electric field that will cause a force of 2.4 × 10−22 N on an electron (qe = −1.602 × 10−19 C)
Answer:
using: 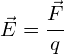
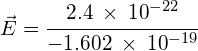
![]() , or
, or
![]() in the opposite direction to the force
in the opposite direction to the force
Example 2:
Calculate the acceleration of the electron in example 1 (mass of an electron = 9.1 × 10−31 Kg):
Answer:
using:
![]() and rearranging to give:
and rearranging to give:
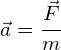
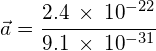
![]()
Example 3:
Calculate the force between 2 protons that are separated by 5mm (qp = 1.602 × 10−19 C):
Answer:
using: 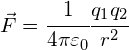
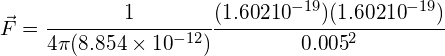
![]() (repulsion)
(repulsion)
