Standing Waves in Strings - Learn

Standing Waves in Strings

Standing or stationary waves form on strings when travelling waves on the strings vibrate at the resonant frequencies of the string. The resonant frequencies produced by these vibrations which produce standing waves are known as harmonics. The simplest form of vibration, consisting of one antinode is called the fundamental frequency or first harmonic. The other modes of vibration are known as the second harmonic, third harmonic and so on. Other than the first harmonic, all other harmonics are known as overtones.

The resonant frequencies or harmonics in a string length can be determined by the relationship between the length of the string $l$ , and the wavelength $\lambda$ , of the corresponding standing wave:

$\lambda =\cfrac { 2l }{ n }$

where:

$\lambda$ = the wavelength in metres (m)

$l$ = the length of the string in metres (m)

$n$ = the number of harmonics, which is also the number of antinodes (1, 2, 3, 4 etc)

The relationship between $\lambda$ , $l$ and $n$ is illustrated below:

Another equation derives from the relationship: $v=f\lambda$ . This equation allows the frequency of the standing wave to be determined:

$f=\cfrac { nv }{ 2l }$

where:

$f$ = the frequency of the wave in Hertz (Hz)

$v$ = the velocity of the wave in ${ m }/{ s }$

$l$ = the length of the string in metres (m)

$n$ = the number of harmonics, which is also the number of antinodes (1, 2, 3, 4 etc)

A third equation considers the tension of the string and how it impacts the velocity of the wave:

$v=\sqrt { \cfrac { T }{ \cfrac { m }{ l } } } =f\lambda$

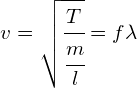
where:

$T$ is the tension in the string in Newtons (N)

$\cfrac { m }{ l }$ = the mass per unit length in ${ kg }/{ m }$

$v$ = the velocity of the wave in ${ m }/{ s }$

$f$ = the frequency of the wave in Hertz (Hz)

$l$ = the length of the string in metres (m)

Example 1:

The first harmonic of a 1.6m long piece of string fixed at both ends is 25Hz.

a) What are the frequencies of the second, third and fifth harmonic?

b) What is the speed of the waves in the string?

c) What is the wavelength of the first harmonic?

d) Is it possible to have a frequency of 40Hz?

Answers:

a) The frequency of each harmonic is the harmonic number times the fundamental frequency:

Second harmonic: $2\times 25=50Hz$

Third harmonic: $3\times 25=75Hz$

Fifth harmonic: $5\times 25=125Hz$

b) Using: $f=\cfrac { nv }{ 2l }$ and rearranging to give: $v=\cfrac { 2lf }{ n }$

$v=\cfrac { 2\times 1.6\times 25 }{ 1 }$

$v=80\; { m }/{ s }$

c) The first harmonic represents half of a wavelength, therefore:

$\lambda=2l$

$\lambda=2\times 1.6m$

$\lambda=3.2m$

d) The first and second harmonic are 25Hz and 50Hz respectively. Therefore, 40Hz is not a frequency of one of the harmonics and will not represent one of the standing waves on this string under the same tension.

Example 2:

A string on a guitar is 50cm long and has a mass of 10g. The tension in the string is 200N.

a) What is the velocity of the wave in this string?

b) What is the fundamental frequency of this string?

c) What effect does increasing the tension have on the velocity of the wave in the string?

Answers:

a) using: 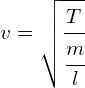$v=\sqrt { \cfrac { T }{ \cfrac { m }{ l } } }$

$v=\sqrt { \cfrac { 200 }{ \cfrac { 0.01 }{ 0.5 } } }$

$v=100\;{ m }/{ s }$

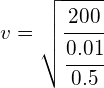
b) using: $f=\cfrac { nv }{ 2l }$

$f=\cfrac { 1\times 100 }{ 2\times 0.5 }$

$f=100$ Hz

c) Increasing the tension will increase the numerator in the equation: 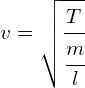$v=\sqrt { \cfrac { T }{ \cfrac { m }{ l } } }$ . The result of this will be a higher velocity.