Interference and Young's Experiment - Learn

Interference and Young’s Experiment – Learn

Interference occurs as a result of two waves interacting. For the purpose of this section, we will consider the interacting waves to have identical properties. Two identical waves interfering will produce sections of increased wave height, decreased wave height and even a wave height = 0. Interference can be considered as constructive or destructive:

Constructive interference occurs when the waves interact to produce an increased amplitude. This happens when the waves are of equal frequency and in phase so that the amplitudes of the waves add together.

Destructive interference occurs when the waves interact to produce a decreased amplitude. This happens when the waves are of equal frequency but are not in phase, producing an amplitude equal to the subtraction of the waves.

Diffraction

In this section, interference patterns are observed as a result of diffraction. Diffraction is the bending and spreading of waves as they pass through a gap or around obstacles. Diffraction is why you can still hear sound waves from a speaker in another room, or why a water wave will spread through marina that has a small gap to the ocean.

Diffraction and slit width

Diffraction is significant when the size of the opening or obstacle is similar to or smaller than the wavelength of the wave. When the slit width is much greater than the wavelength than diffraction only occurs at the edges.

The following diagram illustrates how diffraction occurs at a gap that is a) larger than the wavelength, and b) smaller than the wavelength:

Interference and Light

When interference occurs with light it produces bands of light and dark when displayed on a screen. Huygens observed these light and dark bands around the edges of shadows, and correctly explained them in terms of light diffracting and then interfering to form patterns. Huygens was not able to make accurate measurements with any significance, so his explanations were not supported too strongly. Thomas Young conducted an experiment which provided the quantitative evidence for the interference of light. He achieved this by designing an experiment that used just two point sources of monochromatic (single-wavelength) light. This was known as Young’s double slit experiment.

Young’s Experiment

In 1803, Young performed an experiment in which he shone monochromatic light (only one colour) through a small pin hole. He placed a converging lens behind the hole so that the cone of sunlight became a parallel beam of light. This narrow beam of light was projected onto a screen containing two very tiny slits. On the far side of the double slits he placed another screen, on which he observed the pattern produced by the light passing through the slits. Young observed a series of bright and dark bands or ‘fringes’. This contrasted with Newtons theory which predicted that the light particles would pass directly through and produce two smaller narrow beams.

Young explained this bright and dark pattern by treating light as a wave. He assumed that the monochromatic light was like plane waves and that, as they passed through the narrow slits, these plane waves diffracted into coherent circular waves which were in phase. The circular waves would interact causing interference. The interference pattern produced by these two waves would result in lines of constructive (bright spots) and destructive (dark spots) interference that would match the bright and dark fringes that he had observed.

The bright and dark bands were a result of a change in path difference of the interfering waves:

Analysing Young’s Experiment

If we analyse waves from the different slits meeting at a particular point on the screen, the waves have travelled from their sources (slits) along two alternative routes. The difference between the lengths of the two paths is called the path difference. If the path difference is different by a half of a wavelength, crests of the wave from one slit always meet the troughs of the wave from the other slit (that is, they are out of phase by 180°). This results in destructive interference occurring and a dark band will be produced on the screen. Destructive interference occurs when the path difference is a whole number, minus one half, multiplied by the wavelength of the light: (n − 0.5)𝜆 where n = 1, 2, … and is the number of bright bands from the central bright band. A bright band occurs when, in spite of a path difference, the waves are in phase: crests reinforcing crests and troughs reinforcing troughs.

Constructive interference occurs when the path difference is a whole number multiple of the wavelength of the light, n𝜆, again where n = 1, 2, … and is the number of bright bands from the central bright band.

Destructive interference of coherent waves occurs when the path difference equals an odd number of half wavelengths: pd= ( m − 1/2 )λ, where m = 1, 2, 3 ..
Constructive interference of coherent waves occurs when the path difference equals a whole number of wavelengths: pd= mλ, where m = 0, 1, 2, 3 …

The diagram below illustrates the geometry of Young’s experiment.

Two rays D1 and D2 are meeting at point P and interfering constructively to produce a maximum, that is, a bright spot. As this is the first bright spot counted from the central bright spot (n=1), the extra distance travelled by ray D2 must be equal to m𝜆. It can also be seen that this path difference is equal to dsin𝜃 by trigonometry. Hence, for constructive interference or maximum:

$d\sin { \theta } =m\lambda$

where:

$d$ is the slit separation (in m)

$\theta$ is the angle between the bright point on the screen and a perpendicular line bisecting the slits.

$m$ is any whole number: 0, 1, 2, 3 etc

$\lambda$ is the wavelength of the light waves

Determining the Distance Between Bright Spots

Using the diagram and extending on the geometry outlined above, we can derive an equation that can be used to determine the distance between bright spots, x. This distance can also be used to determine the distance between any number of bright spots.

$\sin { \theta } =\cfrac { m\lambda }{ d } =\cfrac { x }{ L }$

where:

$x$ is the distance between bright spots (in m)

$L$ is the distance from the slits to the screen (in m)

Example 1:

A light source produces monochromatic light of wavelength 540 nm. The light falls on parallel, vertical slits that are 0.075mm apart, an interference pattern is observed on a screen 2.00m away. The pattern shows a series of bright and dark bands.

a) Determine the angle of the first-order maximum, and the distance on the screen of that maximum from the central maximum.

b) Determine the distance from the central maximum to the fourth-order maximum.

Answers:

a) First order maximum occurs when m=1, therefore rearranging:

$d\sin { \theta } =m\lambda$ to give: $\theta =\sin ^{ -1 }{ \cfrac { m\lambda }{ d } }$

$\theta =\sin ^{ -1 }{ \cfrac { 1\times (540\times { 10 }^{ -9 }) }{ 7.5\times { 10 }^{ -5 } } }$

$\theta ={ 0.413 }^{ \circ }$

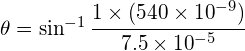
The distance from the central maximum to the first-order maximum is given by:

$x=L\sin { \theta }$

$x=2.00\times \sin { 0.413 }$

$x=0.0144\:m$

$x=14.4\:mm$

b) As the maxima are equally spaced, the distance to the fourth-order maximum is four times the distance to the first.

Therefore, the distance to fourth-order maximum = 4 × 14.4 mm = 57.7 mm