Relativistic Momentum and Maximum Velocity - Learn

Relativistic Momentum and Maximum Velocity – Learn

Relativistic Mass

Einstein showed that length and time were relativistic. He also believed that the third physical quantity of mass would also be relative. Einstein determined that the mass of an object would increase as its speed increased toward relativistic speeds. The relative mass of an object is given by:

$m\:=\:\cfrac { { m }_{ 0 } }{ \sqrt { 1-\cfrac { { v }^{ 2 } }{ { c }^{ 2 } } } }$

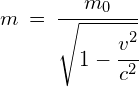
Where:

$m$ = the mass in the stationary frame

${ m }_{ 0 }$ = the rest mass. This is the mass as measured when the mass is stationary in an inertial frame of reference.

$v$ = the speed of the moving frame of reference

$c$ = the speed of light

Relativistic Momentum

In classical physics, the momentum of an object is given by: p=mv. At relativistic speeds, as mass becomes relative, the momentum of an object also becomes relative. We can use the following equation for the objects relativistically corrected momentum:

$p\: =\: \cfrac { { m }_{ 0 }v }{ \sqrt { 1-\cfrac { { v }^{ 2 } }{ { c }^{ 2 } } } }$

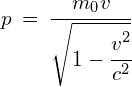
Einstein explored the problems that the idea of relativistic momentum posed by extending on the Newtonian ideas of force and momentum. The following graph illustrates how as the velocity increases the relative momentum increases.

As the velocity approaches c, the relative momentum approaches infinity. There are two main consequences for this that Einstein saw problems with:

As the speed of a body approaches c, the mass and momentum approach infinity – any constant force that was applied would see the acceleration of the object approach 0.
As the velocity of a body approaches c the relative mass also approaches infinity and this would require an ever increasing force to maintain larger and larger accelerations.

The final result of this is that an object can theoretically approach but never actually achieve a speed of c.

Consequences of Relativistic Momentum

Newtonian physics is useful at low velocities where the effects of relativity are negligible. There are factors which become observable at relativistic speeds which need to be considered:

Relativistic momentum is important in particle accelerators where subatomic particles are accelerated to speeds approaching the speed of light. The force required to accelerate the particles at a constant rate increases with speed. This requires huge amounts of energy and the costs of developing and maintaining the equipment is significant.

Consideration has to be given to the particle itself in experiments as the particles interact as though they have a much larger mass. As their relative mass increases it also becomes harder to make the particle follow a circular path.

Example 1:

What is the momentum of a proton moving at 0.85c relative to an observer?

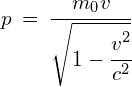
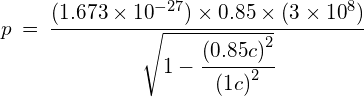
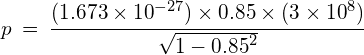
using: $p\: =\: \cfrac { { m }_{ 0 }v }{ \sqrt { 1-\cfrac { { v }^{ 2 } }{ { c }^{ 2 } } } }$

$p\: =\: \cfrac { (1.673\times { 10 }^{ -27 })\times 0.85\times (3\times { 10 }^{ 8 }) }{ \sqrt { 1-\cfrac { { (0.85c) }^{ 2 } }{ { (1c) }^{ 2 } } } }$

$p\: =\: \cfrac { (1.673\times { 10 }^{ -27 })\times 0.85\times (3\times { 10 }^{ 8 }) }{ \sqrt { 1-{ 0.85 }^{ 2 } } }$

$p\: =\: \cfrac { 4.266\times { 10 }^{ -19 } }{ 0.5268 }$

$p\: =\: 8.1\times { 10 }^{ -19 }\: kg\:{ ms }^{ -1 }$