deBroglie's Matter Waves - Learn

de Broglie’s Matter Waves – Learn

Before detailing de Broglie’s contribution to quantum physics, it will be useful to understand a specific advancement in physics that underpins the experimental analysis which confirmed his hypothesis.

Bragg’s Law

In the early 20^th century, a father and son jointly earned a Noble Prize for their explanation of interference patterns when X-rays collided with a range of solids. William Henry Bragg and William Lawrence Bragg projected radiation of a known wavelength at crystal lattice structures, found mostly in metals, and proposed a relationship between the wavelength of the radiation, the spacing in the lattice structure and the angle at which the radiation strikes the material. This became known as Bragg’s Law.

This is the crystal structure of a metal salt (sodium chloride), showing the repeating lattice of ions. In Bragg’s experiments, X-rays interacting with different layers of this lattice had a path difference (travelling different distances), becoming out of phase. Consequently, interference patterns were observed.

de Broglie’s proposal

Louis de Broglie was a French physicist who made great contributions to quantum mechanics. Following World War I, he applied himself to studying the photoelectric effect. Einstein explained the photoelectric effect in 1905, and following confirmation of his theories experimentally by Robert Millikan, he was awarded the Nobel Prize in 1921. As previously discussed in this course, Einstein explained the photoelectric effect through light being quantized, containing a specific amount of energy, and behaving like a particle. This did not dispel the many instances where light was readily observed to behave as a wave, but meant the light had a dual nature, exhibiting both particle and wave properties.

In the early 1920s, de Broglie extended the duality of light proposed by Einstein. He suggested that the notion of duality should be “generalized by extending it to all material particles and notably electrons”. Combining aspects of relativity and the photoelectric effect, he derived an expression for the wavelength of matter.

From a relativity perspective, an expression for the momentum of a photon can be attained.

$p=\cfrac{E}{c}$

The energy of a photon can also be represented through Planck’s model, and the photoelectric effect.

$E=hf$

$E=\cfrac{hc}{\lambda }$

$\cfrac{E}{c} =\cfrac{h}{\lambda }$

Through equating these expressions, the following relationship is derived for a photon.

$\lambda =\ \cfrac{h}{p}$

de Broglie proposed that an electron should behave the same.

$\displaystyle \lambda _{e} =\cfrac{h}{p_{e}}$

$\displaystyle \lambda _{e} =\cfrac{h}{m_{e} v_{e}}$

It did not take long for his theories to be supported by empirical observations, even if by accident initially.

Davisson and Germer

In the late 1920s, two American physicists, Clinton Davisson and Lester Germer, were examining the surface of nickel by firing high speeds electrons at it and recording how they bounced off the surface. The experiment was conducted in a vacuum chamber, to minimise the impact of other atoms, and collected data using a movable electron detector. The basic apparatus is displayed below.

At a point during their investigations, the nickel target was corroded. To remove the corrosion, the nickel was heated to a very high temperature, unbeknownst to Davisson and Germer changing the internal structure of the nickel. It formed a simple crystal lattice, which made observable interference patterns noticeable with the detector. This became the first observation of matter exhibiting a wave-like property. Through further analysis, this became the first evidence of de Broglie’s proposal, with his equation supporting the analysis of the interference patterns through Bragg’s Law.

The image below shows the output of a modern electron diffraction experiment, where a stream of electrons is passed through a lattice structure only one atom thick. A florescent screen then shows the trajectory of these diffracted electrons. From left to right the velocity of the electrons has been increased, hence reducing the wavelength of the electron according to de Broglie’s equation. The decreasing wavelength causes the angle between bright spots to narrow, similar to the impact of changing wavelength in Young’s double slit experiment from Module 7.

Observing matter waves

It is very difficult to observe matter behaving as a wave on an everyday scale due to the extremely small wavelengths involved. In Example 1, an electron travelling just over 1% of the speed of light was observed to have a wavelength about one million times smaller than that of visible light. Consider the following example to put this further into perspective.

Example 1:

Determine the wavelength of an electron after it has been accelerated from rest by a voltage of 5000V.

Calculating velocity

$W=qV$

$K=\cfrac{1}{2} mv^{2}$

$W=K$

$qV=\ \cfrac{1}{2} mv^{2}$

$v=\sqrt{\cfrac{2qV}{m}}\\$

$v=\sqrt{\cfrac{2\times 1.602\times 10^{-19} \times 5000}{9.109\times 10^{-31}}}\\$

$v=\ 4.19\times 10^{6} \ ms^{-1}$

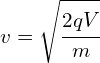
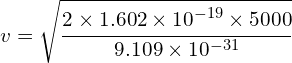
Calculating wavelength

$\lambda =\cfrac{h}{mv}$

$\lambda \ =\cfrac{6.626\times 10^{-34}}{9.109\times 10^{-31} \times 4.19\times 10^{6}}$

$\lambda =1.73\times 10^{-11} m$

Example 2:

The best cricketer players in the world are able to bowl the ball at speeds of up to 45 ms^-1. If a cricket ball has a mass of 156g, what would be the wavelength of a cricket ball travelling at this speed?

$\lambda =\cfrac{h}{mv}$

$\lambda =\cfrac{6.626\times 10^{-34}}{0.156\times 45}$

$\lambda =9.44\times 10^{-35} m$

The wavelength determined in Example 2 is about five Planck lengths, which is the smallest possible distance in the universe. When it is taken into account that an a hydrogen atom is about 10²⁵ Planck lengths in diameter, it puts into perspective the insignificance of wavelengths of everyday objects in motion.