Calculating Magnetic Fields – Learn
The strength of the magnetic field around a current-carrying conductor and a solenoid can be determined quantitatively.
- The equation used to calculate the strength of the field around a current-carrying conductor, gives us the magnitude of the field at some distance,
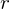 , from the conductor.
, from the conductor. - The equation used to calculate the strength of the field in a solenoid, gives us the magnitude of the field at a point inside of the solenoid. The field within the solenoid is uniform.
Current-carrying conductors
The magnitude of the field (![]() ) at some distance,
) at some distance, ![]() , from the current-carrying conductor is given by:
, from the current-carrying conductor is given by:
![]()
where:
![]() = the strength of the magnetic field (in Tesla)
= the strength of the magnetic field (in Tesla)
![]() = the permeability of free space (
= the permeability of free space (![]() )
)
![]() = the current in the wire (in amps)
= the current in the wire (in amps)
![]() = the radius, or distance from the wire (in m)
= the radius, or distance from the wire (in m)
Solenoids
The magnitude of the field (![]() ) within a solenoid is given by:
) within a solenoid is given by:
![]()
where:
![]() = the strength of the magnetic field (in Tesla)
= the strength of the magnetic field (in Tesla)
![]() = the permeability of free space (
= the permeability of free space (![]() )
)
![]() = the number of turns in the coil
= the number of turns in the coil
![]() = the current in the wire (in amps)
= the current in the wire (in amps)
![]() = the length of the solenoid (in m)
= the length of the solenoid (in m)
Example 1:
What is the strength of a magnetic field at a distance of 5cm from a wire carrying a current of 10A?
Answer:
![]()
where:
![]() = (
= (![]() )
)
![]()
![]()
![]()
![]()
Example 2:
What is the strength of a magnetic field in a 15cm solenoid that has 250 turns carrying a current of 20A?
Answer:
![]()
where:
![]() = (
= (![]() )
)
![]()
![]()
![]()
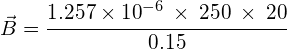
![]()
