Work Done by Forces
Work
Work is done whenever energy is changed from one form to another. For example, when a rock is picked up into the air, chemical energy in your muscles changes into gravitational potential energy when the rock is in the air. If you drop it and it falls back down to Earth, the gravitational potential energy changes back into kinetic energy. Work done is measured in joules (J).
Work and force
When energy changes form, a force is involved. In the example above, somebody has to apply a force to pick the rock up. From that point onwards, gravity applies a downward force to the rock as it returns to Earth.
In general:
Work done = change in energy, ![]() measured in joules, J
measured in joules, J
Calculating Work Done
In general: ![]()
Where;
![]() = work done in J
= work done in J
![]() = applied force in N
= applied force in N
![]() = distance object moves in m
= distance object moves in m
Different problems may require other derivations of ![]() ;
;
- An object that changes velocity:
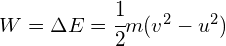
- An object that changes its height:
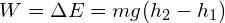
Example 1:
A person applies a force of 25N to push a box 8m across the floor. Calculate the work done on the box:
![]()
![]()
![]()
Example 2:
A child pulls a billycart with a force of 10N. They do 250J of work. How far have they pulled the billycart?
![]()
![]()
![]()
![]()
Example 3:
A cyclist accelerates from ![]() to
to ![]() . How much work was done if the mass of the bike and the cyclist was 100kg?
. How much work was done if the mass of the bike and the cyclist was 100kg?
Recalling that; ![]() and;
and;
![]()
![]()
![]()
Example 4:
A floorman lifts a 8kg box from the floor to a shelf which is 1.2m above floor level. Calculate the work done on the box:
Recalling that; ![]() and;
and;
![]()
![]()
![]()
