Orbital Motion of Planets and Satellites – Learn
Newton’s law of universal gravitation can be used to derive an equation for the average orbital speed, (![]() ) of a planet (secondary body) around the Sun (primary body).
) of a planet (secondary body) around the Sun (primary body).
The gravitational force (![]() ) between the Sun and a planet is the force that is responsible for the centripetal force (
) between the Sun and a planet is the force that is responsible for the centripetal force (![]() ) on the planet, keeping it in orbit around the Sun:
) on the planet, keeping it in orbit around the Sun:
![]()
![]()
where:
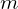 is the mass of the secondary body in kg
is the mass of the secondary body in kg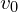 is the orbital velocity of the secondary body in
is the orbital velocity of the secondary body in 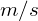
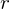 is the distance between the centre of mass of the two bodies in m
is the distance between the centre of mass of the two bodies in m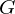 is the universal gravitational constant =
is the universal gravitational constant = 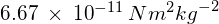
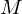 is the mass of the primary body in kg
is the mass of the primary body in kg
dividing by m
![]()
multiplying by r
![]()
taking the square root of each side
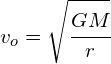
note: that the orbital speed does not depend on the mass of the satellite. It is proportional to the square root of the mass of the primary body and inversely proportional to the square root of the distance between the bodies.
The equation for orbital velocity can also be extended to satellites in orbit around Earth. Note that the radius, ![]() , is the sum of the radius of the Earth and the altitude of the satellite. Thus, the equation becomes:
, is the sum of the radius of the Earth and the altitude of the satellite. Thus, the equation becomes:
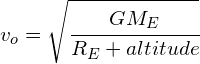
Period of Orbit
The period of orbit can be determined using:
![]()
Example 1:
Calculate the orbital velocity of the Moon given the following information:
- Mass of the Earth
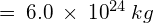
- Mass of the Moon
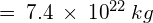
- Average Earth – Moon distance
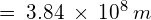
Answer:
Using: (note that the mass of the secondary body (the moon) is irrelevant)
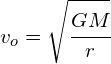
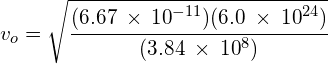
![]()
Example 2:
A satellite orbits the Earth at an altitude of 400km. Use the following information to calculate:
a) the orbital velocity of the satellite
b) the period of the satellite
- Mass of the Earth,
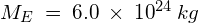
- Radius of the Earth,
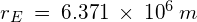
Answers:
a) Using: 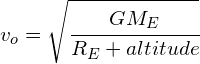
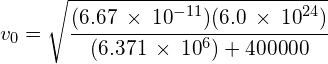
![]()
b) Using: ![]()
Where: ![]() m
m
![]()
![]()
![]()
![]()
