Uniform Circular Motion – Learn
Uniform circular motion occurs when an object travels in a circle at a constant speed.
- The period (T) is the time it takes for the object to make one complete revolution.
- The distance (d) completed during one revolution is the circumference of the circle (
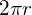 ).
).
The average speed of the object is given by: ![]()
The object in circular motion is travelling at a constant speed but its changing direction constantly, therefore the velocity of the object is also changing. The magnitude of the velocity remains constant.
Centripetal acceleration
Since the object’s velocity is constantly changing, the object must be accelerating. The direction of this acceleration is toward the centre of the circle and it is constant. This acceleration is called centripetal acceleration.
The centripetal acceleration of the object is given by: ![]()
where:
![]() = the centripetal acceleration in
= the centripetal acceleration in ![]()
![]() = the velocity in
= the velocity in ![]()
![]() = the radius of the circle in
= the radius of the circle in ![]()
Centripetal force
As the object in uniform circular motion is accelerating, it must have some net force acting on it.The direction of this force is also toward the centre of the circle and it is constant. This net force is known as the centripetal force.
The centripetal force acting on the object is derived from: ![]() :
:
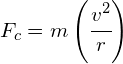
where:
![]() = the centripetal force in
= the centripetal force in ![]()
![]() = the velocity in
= the velocity in ![]()
![]() = the radius of the circle in
= the radius of the circle in ![]()
Average angular velocity
The diagram below illustrates angular velocity. While each point on the red arm travels at a different velocity, each point moves through the same angular displacement (![]() ) in the same period of time.
) in the same period of time.
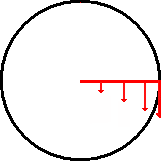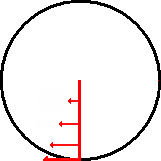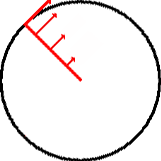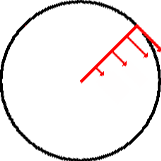
This rate of change of angular displacement is the average angular velocity (![]() )
)
![]()
where:
![]() = angular velocity in
= angular velocity in ![]() or
or ![]()
![]() = the angular displacement in
= the angular displacement in ![]() (one revolution =
(one revolution = ![]() )
)
![]() = time in
= time in ![]()
*note: in this equation, t is the time taken for the angular displacement and not the period, T.
Example 1:
A ball is attached to a string and swung around in uniform circular motion. The length of the string is 1.2m and the mass of the ball is 0.25 kg. The ball completes one complete revolution in 0.4 seconds. Calculate:
a) the magnitude of the velocity of the ball
b) the centripetal acceleration
c) the centripetal force
Answers:
a) using: ![]()
![]()
![]()
b) using: ![]()
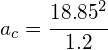
![]() toward the centre of the circle
toward the centre of the circle
c) using: 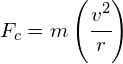
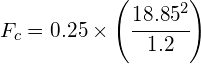
![]() toward the centre of the circle
toward the centre of the circle
Example 2:
The wheel of a bike completes 100 revolutions in 40 seconds. Determine the average angular velocity in:
a) rad/s
b) deg/s
Answers:
using: ![]()
a) ![]()
![]()
b) ![]()
![]()
