Force and Potential Energy in Gravitational Fields – Learn

Gravitational Potential Energy

The gravitational potential energy for objects near the surface of the Earth, U=mgh. In these situations we say that U=0 at ground level. As work is done to lift the object against the gravitational field, U increases as the height, h, increases. This is useful for objects which are close to the surface of the Earth but is not useful for interactions or situations where the gravitational field is not constant.

The equation for gravitational potential energy for any two objects with mass that are a distance, r, apart:

U=-\cfrac { GMm }{ { r } }

Where:

  • M is the mass of the planet in kg
  • m is the mass of the object in kg

  • r is the distance separating the masses in m.

The equation is negative because according to the equation, at some point where r=\infty , U=0. Now as r decreases (or as the objects become closer together), the object loses potential energy. If U decreases from 0, it must become negative! This key difference arises as for objects near the surface of the Earth, we assign ground level to be zero potential. For objects in space, we assign zero potential to be at a position very, very far away, that is, at \infty .

Derivation of Gravitational Potential Energy

Work is done to move an object away from a planet (work is done against the gravitational field). The work done on the object is equal to the change in potential energy of the object. If we are to derive the expression for gravitational potential energy, we need to equate work and gravitational potential energy in terms of G, M, m and r:

W=Fs

W=-\cfrac { GMm }{ { { r }^{ 2 } } } \times \Delta r

W=-\cfrac { GMm }{ { r } }

U=-\cfrac { GMm }{ { r } }

Escape Velocity

Isaac Newton conducted a thought experiment: If he was to throw a stone off the top of a tall building it will fall toward and strike the Earth. If he was to throw it harder, it would travel further before hitting the ground. Newton proposed that if he was able to throw it hard enough it would fall back toward the Earth as the Earth curved away, meaning that it would never actually hit the Earth.

With a similar analogy, we can consider throwing a stone straight up into the air. As we throw it harder it will travel faster. As we throw it faster and faster, it will travel higher and higher. If thrown fast enough it should rise up and continue to rise and slow down but never fall back to Earth. It will finally come to rest only when it has completely escaped the Earth’s gravitational field. The initial velocity required to achieve this is known as escape velocity. This is the minimum speed that an object at the surface of the Earth will require if it is to escape into space and not be pulled back.

{ v }_{ esc }=\sqrt { \cfrac { 2GM }{ r } }

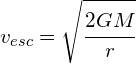
Derivation of Escape Velocity

Escape velocity, vesc, from a large body of mass M is achieved when the total orbital energy of an object is equal to 0, that is:

{ E }_{ k }+U=0

\cfrac { 1 }{ 2 } m{ v }_{ esc }^{ 2 }-\cfrac { GMm }{ r } =0

\cfrac { 1 }{ 2 } m{ v }_{ esc }^{ 2 }=\cfrac { GMm }{ r }

{ v }_{ esc }^{ 2 }=\cfrac { 2GM }{ r }

{ v }_{ esc }=\sqrt { \cfrac { 2GM }{ r } }

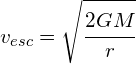
Example 1:

Given the following data, determine the gravitational potential energy of the Moon within the Earth’s gravitational field.

  • Mass of the Earth = 6.0 × 1024 kg
  • Mass of the Moon = 7.35 × 1022 kg

  • Earth–Moon distance = 3.84 × 108 m

Answer:

Using: U=-\cfrac { GMm }{ { r } }

U=-\cfrac { (6.67\times 1{ 0 }^{ -11 })(6.0\times { 10 }^{ 24 })(7.35\times { 10 }^{ 22 }) }{ { (3.84\times { 10 }^{ 8 }) } }

U=-7.66\times { 10 }^{ 28 }\:J

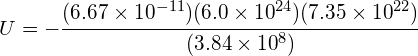
This is the amount of energy required to move the moon from a very large distance away to its position in orbit around the Earth. The negative sign indicates that the work is done by the field.

Example 2:

Calculate the escape velocity for Earth (assume mass of the Earth = 6.0 × 1024 kg and radius of the Earth = 6.371 × 106 m).

Answer:

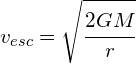
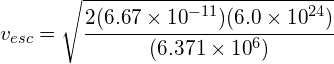
Using: { v }_{ esc }=\sqrt { \cfrac { 2GM }{ r } }

{ v }_{ esc }=\sqrt { \cfrac { 2(6.67\times { 10 }^{ -11 })(6.0\times { 10 }^{ 24 }) }{ (6.371\times { 10 }^{ 6 }) } }

{ v }_{ esc }=\sqrt { 125631769 }

{ v }_{ esc }=11209\: { m }/{ s }

({ v }_{ esc }=40350\: { km }/{ hr })