The Equilibrium Expression, Keq - Learn

The Equilibrium Expression, K_eq

The equilibrium constant, K_eq, is a mathematical relationship between the concentrations of reactants and products in a system when they are at equilibrium at a certain temperature. K_eq is temperature dependent but pressure and catalysts do not have an impact on the value of K_eq.

The general expression for K_eq can be written as:

${ K }_{ eq }=\cfrac { \left[ products \right] }{ \left[ reactants \right] }$

When calculating K_eq, both the concentration of species and the molar ratio from the chemical formulae are important. Consider the general reaction expression below:

$aA\quad +\quad bB\quad \rightleftharpoons \quad cC\quad +\quad dD$

The equilibrium constant, K_eq would be written as follows:

${ K }_{ eq }=\cfrac { \left[ { C }^{ c } \right] \left[ { D }^{ d } \right] }{ \left[ { A }^{ a } \right] \left[ { B }^{ b } \right] }$

Only species that have concentrations which can vary are included in the expression. Aqueous solutions and gases can have concentrations which vary so are included in the calculation of K_eq. Solids and pure liquids are not included.

Homogenous Equilibrium

Homogenous equilibrium systems are ones where all substances are in the same phase. In homogenous systems where all species are in the same phase, solids and liquids are included in the calculation of the equilibrium expression, however, these systems are uncommon in this course.

It is common to see solids and pure liquids as part of a heterogenous equilibrium (different phases) and so are not included in the calculation of K_eq in these instances.

Magnitude of K_eq.

The value of K_eq has no units but the magnitude of this value can tell us where the equilibrium position lies. That is, if there is a higher proportion of reactants or products present at equilibrium.

K_eq has values between 0 and a large number generally up to the order of 10⁵. The following are general assumptions we can make about the position of an equilibrium given the value of K_eq:

If K_eq is close to 1 (0.1 – 10) there are relatively equal proportions of both reactants and products.
If K_eq is greater than 1 (10 – 10,000) products will be favoured in the equilibrium.
If K_eq is less than 1 (0.00001 – 0.1) reactants will be favoured in the equilibrium.

K_eq for the Reverse Reaction.

As equilibrium systems involve both a forward and a reverse reaction, there also exists a value for K_eq for each reaction. However, this value is different depending on the rate of reaction and the direction. K_eq for the reverse reaction is simply the inverse K_eq of the forward reaction:

${ K }_{ eq(rev)\quad }=\cfrac { 1 }{ { K }_{ eq(fwd) } }$

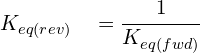
ICE Tables

ICE tables are a common tool which are used to solve equilibrium problems where all of the final equilibrium conditions may not be given. Usually, all of the initial concentrations are given or can be determined along with either the final concentration or the change in concentration of some of the products. This information can be used to determine the final concentrations of all species and this is applied to the equilibrium expression, K_eq.

I – initial concentration
C – change in concentration
E – equilibrium concentration

To determine the final equilibrium concentrations of all reactants and products, the changes in concentration are applied to the balanced equation.

See example 2 below:

Reaction Quotient, Q

The reaction quotient, Q, is used when a system is not at equilibrium and can help determine which way the system may move in order to achieve equilibrium. This will allow us to state if the production of reactants or products is favoured in order to reach equilibrium.

$Q=\cfrac { \left[ { C }^{ c } \right] \left[ { D }^{ d } \right] }{ \left[ { A }^{ a } \right] \left[ { B }^{ b } \right] }$

Comparing K_eq and Q

Comparing the values of Q to a stated value of K_eq for an equilibrium system indicates which way the system may shift:

If Q < K_eq, the equilibrium system will shift to the right to favour the forward reaction. This favours the formation of products over reactants.

If Q > Keq, the equilibrium system will shift to the left to favour the reverse reaction. This favours the formation of reactants over products.

Example 1:

Write the equilibrium expression for the following reaction: 2NO_2(g) ⇌ N₂O_4(g)

Answer:

${ K }_{ eq }=\cfrac { \left[ { N }_{ 2 }{ O }_{ 4 } \right] }{ \left[ { N }{ O }_{ 2 } \right] ^{ 2 } }$

Example 2:

PCl_5(g), PCl_3(g) and Cl_2(g)exist together in an equilibrium according to the following equation:

PCl_5(g) ⇌ PCl_3(g) + Cl_2(g)

0.50 moles of PCl_5(g) were placed into a 2L container. At equilibrium, there were 0.20 moles of PCl_5(g) remaining. Complete an ICE table to determine the final concentrations of each component and use this to calculate K_eq:

Answer:

	[PCl_5(g)]	[PCl_3(g)]	[Cl_2(g)]
Initial	0.50/2 = 0.25M	0	0
Change	– 0.20/2 = 0.10	+ 0.10	+0.10
Equilibrium	0.15	0.10	0.10

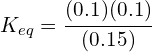
${ K }_{ eq }=\cfrac { (0.1)(0.1) }{ (0.15) }$

${ K }_{ eq }=0.07$