Magnetic Flux Through an Area - Learn

Magnetic Flux Through an Area – Learn

Experiments conducted by Hans Christian Orsted and Michael Faraday in the 19th century concluded that there was a link between electric and magnetic fields. Faraday discovered that a changing magnetic field can produce an electric current. The creation of an electric current as a result of a changing magnetic field is known as electromagnetic induction.

The current that Faraday observed was produced by what’s known as an emf, ε. The term emf is derived from electromotive force but it is more correct to think of emf as a voltage, or a potential difference rather than a force.

Magnetic Flux

To understand how a changing magnetic field can induce an electric current, it is important to first look at the ‘amount of magnetic field’. The amount of magnetic is known as magnetic flux.

Magnetic flux is the name given to the amount of magnetic field passing through a given area. It is given the symbol 𝜙 and is measured in weber (Wb).

The strength of a magnetic field, B, is known as the magnetic flux density. It is the amount of magnetic flux passing through a unit area. Recall that the strength of a magnetic field, B is measured in tesla (T) and now also, weber per square metre (Wbm⁻²).

Faraday pictured a magnetic field consisting of a series of field lines. The density of these field lines represents the magnetic flux density and the number of field lines through any particular area represents the magnetic flux. Note: we could have equal amounts of magnetic flux through different sized areas. For example, a small area with a large magnetic flux density could have the same magnetic flux as a large area with a small magnetic flux density.

Calculating Magnetic Flux

The equation used to calculate the magnetic flux, 𝜙, is:

$\phi ={ B }_{ \parallel }A=BA\cos { \theta }$

where:

$\phi$ is the magnetic flux (in Wb)

${ B }_{ \parallel }$ is the strength of the magnetic field parallel to the area vector (in T)

$A$ is the area vector (in m²)

${ \theta }$ is the angle between the magnetic field and the normal to the area vector*

*note: this definition is important. Many students incorrectly measure θ as the angle between the plane of the area vector and the magnetic field lines. (see below)

The diagram below illustrates the following situations:

θ = 0° (magnetic flux is a maximum)
θ = 90° (magnetic flux is a minimum)
θ = θ° (magnetic flux, $\phi =BA\cos { \theta }$ )

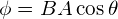note: some questions may give the magnetic field at an angle to the plane of the area/coil. Be sure you can determine the correct angle to use in the equation. The diagram below shows:

θ₁ = the angle between the magnetic field and the area/coil (incorrect θ)
θ₂ = the angle between the magnetic field and the normal to the area/coil (correct θ)

Example 1:

A square coil with sides of 10cm is placed in a magnetic field with a strength of 0.4T. Calculate the magnetic flux if:

a) The coil is perpendicular to the field

b) The plane of the coil is at 20° to the field

Answers:

a) If the coil is perpendicular to the field, the normal to the coil must be parallel to the field, therefore θ = 0°. Also the area, A, of the coil = 0.1m × 0.1m = 0.01m²

using: $\phi =BA\cos { \theta }$

$\phi =0.4\: \times \:0.01\cos { { 0 }^{ \circ } }$

$\phi =0.004\:Wb$

b) If the plane of the coil is 20° to the field, the angle between the normal to the coil and the field must be = 70°

using: $\phi =BA\cos { \theta }$

$\phi =0.4\: \times \:0.01\cos { { 70 }^{ \circ } }$

$\phi =0.0014\:Wb$

$\phi =0.001\:Wb$