Forces Between Parallel Conductors - Learn

Forces Between Parallel Conductors – Learn

When a wire has a current flowing through it a magnetic field will result around the wire. The magnetic field forms circular loops around the wire which decrease in strength as the distance from the wire increases. The direction of the magnetic field is determined using the right hand grip rule:

wrap fingers around the current carrying conductor
thumb points in the direction that the current flows
fingers indicate the direction of the magnetic field (often described as clockwise or anticlockwise depending on the view)

Two Current Carrying Conductors

When two wires carrying a current are placed parallel to each other, their magnetic fields will interact, resulting in a force acting between the wires. The magnitude of the force acting on each wire is equal, but the directions are opposite. This is true even if the conductors carry currents of different magnitudes.

The diagram below illustrates two examples where the direction of the magnetic field around each wire is drawn with the • × notation. Diagram A shows the current in the wires travelling in the same direction and diagram B shows the current travelling in opposite directions:

Determining the direction of the force

The direction of the force is determined by looking at the direction of the individual fields in the area between the conductors:

Diagram A: fields are opposite resulting in an attractive force
Diagram B: fields are the same resulting in a repulsive force

As a rule; when the current flowing through the conductors is in the same direction the force will be attractive and when the currents are opposite in direction the force will be repulsive.

Determining the magnitude of the force between two parallel conductors

The magnitude of the force acting between two parallel current carrying conductors is impacted by several factors:

The current in each conductor
The length of the conductors
The distance separating the conductors

The magnitude of the force acting between two parallel current carrying conductors is calculated using:

$\cfrac { F }{ l } =\cfrac { { \mu }_{ 0 } }{ 2\pi } \cfrac { { I }_{ 1 }{ I }_{ 2 } }{ r }$

Where:

$\cfrac { F }{ l }$ is the force per unit length between the conductors (in Nm⁻¹)

${ \mu }_{ 0 }$ is the magnetic permeability of free space (4π × 10⁻⁷ NA⁻²)*

${ I }_{ 1 }$ is the current in wire 1 (in A)

${ I }_{ 2 }$ is the current in wire 2 (in A)

$r$ is the distance separating the conductors (in m)

*note: ${ \mu }_{ 0 }=4\pi \times { 10 }^{ -7 }$ and $\cfrac { { \mu }_{ 0 } }{ 2\pi } =2\times { 10 }^{ -7 }$ .

The equation can be written: $F=\cfrac { { kI }_{ 1 }{ I }_{ 2 }l }{ r }$

where $k=2\times { 10 }^{ -7 }\: N{ A }^{ -2 }$

SI definition for electrical current; the ampere and Newton’s Third Law of Motion

The System International (SI) of Units states that the ampere is the unit for electrical current. The formal definition of the ampere is: One ampere is the constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed one metre apart in a vacuum, would produce between those conductors a force equal to 2 × 10⁻⁷N/m of length.

This is an application of Newton’s Third Law of Motion, which states: In a two-body system, if body A exerts a force on body B, then body B exerts a force on body A that is equal in magnitude, but opposite in direction.

Newton’s Third Law of Motion is sometimes stated: For every action there is an equal and opposite reaction. If one wire applies a force to a second wire, the second wire will apply a force that is equal in magnitude and opposite in direction on the first wire.

Example 1:

Two conducting wires, A and B, have currents flowing through them in different directions and are separated by a distance of 4cm. What is the magnitude and direction of the force per unit length acting between the wires if conductor A has a current of 2.5 A and conductor B has a current of 1.5 A?

Using: $\cfrac { F }{ l } =\cfrac { { \mu }_{ 0 } }{ 2\pi } \cfrac { { I }_{ 1 }{ I }_{ 2 } }{ r }$

Where:

I₁ = 2.5 A
I₂ = 1.5 A
r = 0.04 m

$\cfrac { F }{ l } =\cfrac { 4\pi \times { 10 }^{ -7 } }{ 2\pi } \times \cfrac { 2.5\times 1.5 }{ 0.04 }$

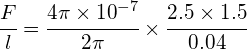
$F={ 1.875\times 10 }^{ -5 }\:N$ (repulsive force)