Newton’s Law of Universal Gravitation – Learn

Newton’s Law of Universal gravitation was based on several principles:

  • Every object in the Universe attracts every other object with a gravitational force
  • The gravitational force is directly proportional to the masses of the objects
  • The gravitational force is inversely proportional to the square of the distance between them

Newton derived a relationship for the magnitude of the gravitational force acting between two objects:

\overset { \rightarrow }{ F } =-\cfrac { GMm }{ \overset { \rightarrow }{ { r }^{ 2 } } }

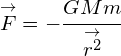
where:

\overset { \rightarrow }{ F } is the gravitational force in N. (The negative sign in the equation indicates that the force is an attractive force)

G is the universal gravitation constant = 6.67\:\times \:{ 10 }^{ -11 }\:N{ m }^{ 2 }{ kg }^{ -2 }

M is the mass of the larger body in kg

m is the mass of the smaller body in kg

r is the distance between the centres of the two masses in m, or, distance apart + the radii of each mass in m

The equation may also be seen or written as: 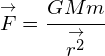\overset { \rightarrow }{ F } =\cfrac { GMm }{ \overset { \rightarrow }{ { r }^{ 2 } } } . Remember to include the direction as attractive.

Calculating gravitational field strength

The strength of the gravitational field experienced by an object on or near the surface of any planet or moon is derived from the previous equation. If we assign a mass of 1kg to our object and also assume: { F }_{ g }={ m }_{ object }\times { g }_{ planet } , we can conclude that:

mg=\cfrac { GMm }{ \overset { \rightarrow }{ { r }^{ 2 } } }

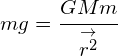
and after cancelling, m, the smaller mass:

g=\cfrac { GM }{ \overset { \rightarrow }{ { r }^{ 2 } } }

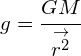
The unit for gravitational field strength is N{ kg }^{ -1 }

Calculating gravitational field strength at altitude

As an object moves from the surface of the Earth (or any planet) to a higher altitude, the strength of the gravitational field will decrease. These problems can be resolved by modifying the previous equation:

g=\cfrac { GM }{ \overset { \rightarrow }{ { ({ R }_{ E }+altitude) }^{ 2 } } }

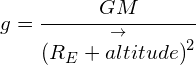
where:

{ R }_{ E } is the radius of the Earth (or any planet)

altitude is the distance that the object is from the surface of the Earth (or any other planet)

Useful constants: The following are given on data sheets and will be useful here:

  • Mass of the Earth, { M }_{ E }\:=\:6.0\:\times \:{ 10 }^{ 24 }\:kg
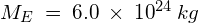
  • Radius of the Earth, { r }_{ E }\:=\:6.371\:\times \:{ 10 }^{ 6 }\:m

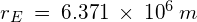
Example 1:

Use the following data to determine the magnitude of the gravitational attraction between the Earth and the Moon:

  • Mass of the Earth =\:6.0\:\times \:{ 10 }^{ 24 }\:kg
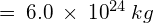
  • Mass of the Moon =\:7.4\:\times \:{ 10 }^{ 22 }\:kg
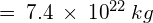
  • Average Earth – Moon distance =\:3.84\:\times \:{ 10 }^{ 8 }\:m

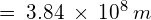
Answer:

\overset { \rightarrow }{ F } =-\cfrac { GMm }{ \overset { \rightarrow }{ { r }^{ 2 } } }

\overset { \rightarrow }{ F } =\cfrac { (6.67\: \times \: { 10 }^{ -11 })(6.0\: \times \: { 10 }^{ 24 })(7.4\: \times \: { 10 }^{ 22 }) }{ { (3.84\: \times \: { 10 }^{ 8 }) }^{ 2 } }

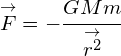
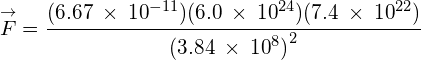
\overset { \rightarrow }{ F } ={ 2.0\times 10 }^{ 20 }\:N (attraction)

Example 2:

Use the following data to determine the gravitational field strength on Mars:

  • Mass of the Mars =\:6.39\:\times \:{ 10 }^{ 23 }\:kg
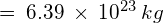
  • Radius of Mars =\:3.39\:\times \:{ 10 }^{ 6 }\:m

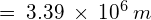
Answer:

g=\cfrac { GM }{ \overset { \rightarrow }{ { r }^{ 2 } } }

g=\cfrac { (6.67\: \times \: { 10 }^{ -11 })(6.39\: \times \: { 10 }^{ 23 }) }{ { (3.39\: \times \: { 10 }^{ 6 }) }^{ 2 } }

g=3.71\: N{ kg }^{ -1 }

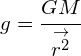
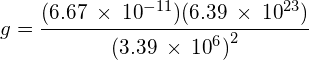
Example 3:

Use the following data to determine the gravitational field strength in a low Earth orbit of 2000km:

  • Mass of the Earth, { M }_{ E }\:=\:6.0\:\times \:{ 10 }^{ 24 }\:kg
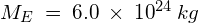
  • Radius of the Earth, { r }_{ E }\:=\:6.371\:\times \:{ 10 }^{ 6 }\:m

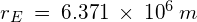
Answer:

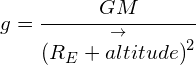
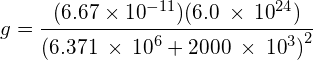
g=\cfrac { GM }{ \overset { \rightarrow }{ { ({ R }_{ E }+altitude) }^{ 2 } } }

g=\cfrac { (6.67\times { 10 }^{ -11 })(6.0\: \times \: { 10 }^{ 24 }) }{ { (6.371\: \times \: { 10 }^{ 6 }+2000\: \times \: { 10 }^{ 3 }) }^{ 2 } }

g=5.71\: N{ kg }^{ -1 }