Projectile Motion Equations - Learn

Projectile Motion Equations – Learn

Projectile Motion Equations

The following equations are applied to projectile motion problems:

$v=u+at$

${ v }^{ 2 }={ u }^{ 2 }+2as$

$s={ ut+\cfrac { 1 }{ 2 } a{ t }^{ 2 } }$

Where:

$u$ = initial velocity in ${ m }/{ s }$

$v$ = final velocity in ${ m }/{ s }$

$t$ = time in $sec$

$s$ = displacement in $m$

$a$ = acceleration due to gravity ( $g=9.8\:{ m }/{ { s }^{ 2 } }$ )

Equations and vector analysis

As projectile motion problems are analysed in their horizontal and vertical vector components, the equations need to be written with subscripts to reflect this analysis – for example: ${ v }_{ y }=u_{ y }+a_{ y }t$

The importance of direction

Projectile motion deals with many variables which are vectors. This means that direction is a very important consideration for the analysis of projectile motion problems.

Horizontal: As projectiles will only ever move in one direction horizontally, we naturally make this direction positive.
Vertically: As projectiles can move in both directions vertically, a direction (up or down) must be noted as positive. All problems analysed here will consider down as positive*. A key result of this is that the acceleration due to gravity will always be positive ( $g=9.8\:{ m }/{ { s }^{ 2 } }$ ).

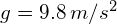*It does not matter which direction you choose to be positive, both will calculate the same answer if direction is consistent throughout the working.

The following are common values that may need to be derived in many projectile motion problems:

Maximum height reached ( $\Delta y$ )
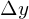Time of flight ( $t$ )
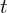Range ( $\Delta x$ )

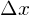These variables are often the link to solving more difficult problems consisting of several parts.

Maximum height reached ( $\Delta y$ )

The maximum height reached considers the vertical part of the projectiles motion. A key point here is that at the maximum height the vertical velocity will be $0$ .

Using the equation: ${ v }^{ 2 }={ u }^{ 2 }+2as$ and writing this with vertical subscripts:

${ v }_{ y }^{ 2 }={ u }_{ y }^{ 2 }+2{ a }_{ y }\Delta y$

Considering the following:

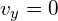${ v }_{ y }=0$ (vertical velocity is 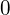$0$ at maximum height)
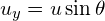${ u }_{ y }=u\sin\theta$ (vertical vector of initial velocity, $u$ )
${ a }_{ y }=g=9.8\:{ m }/{ { s }^{ 2 } }$ )

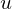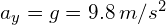We derive the following equation for maximum height:

$0={ u }_{ y }^{ 2 }+2{ a }_{ y }\Delta y$

$0={ (u\sin\theta ) }^{ 2 }+2g\Delta y$

$\Delta y=\cfrac { -{ (u\sin\theta ) }^{ 2 } }{ 2g }$

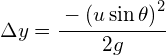
Time of flight ( $t$ )

For a projectile that starts and finishes its trajectory at the same height the total flight time will be 2× the time the projectile takes to reach its maximum height: ${ t }_{ total }\: =\: { 2t }_{ max\: height }$

Using the equation: $v=u+at$ and writing this with vertical subscripts:

${ v }_{ y }=u_{ y }+a_{ y }t$

Considering the following:

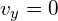${ v }_{ y }=0$ (vertical velocity is 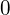$0$ at maximum height)
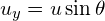${ u }_{ y }=u\sin\theta$ (vertical vector of initial velocity, $u$ )
${ a }_{ y }=g$ ( $g=9.8\:{ m }/{ { s }^{ 2 } }$ )

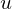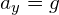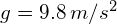We derive the following equation for the time to reach maximum height:

$0=u\sin { \theta } +gt$

$t=\cfrac { -u\sin { \theta } }{ g }$

Considering: ${ t }_{ total }\: =\: { 2t }_{ max\: height }$

${ t }_{ total }=\cfrac { -2u\sin { \theta } }{ g }$

Range ( $\Delta x$ )

The range of a projectile considers the horizontal part of the projectiles motion. A key point here is that the projectile has a constant horizontal velocity

Using the equation: $s={ ut+\cfrac { 1 }{ 2 } a{ t }^{ 2 } }$ and writing this with horizontal subscripts:

$\Delta x={ { u }_{ x }t+\cfrac { 1 }{ 2 } { a }_{ x }{ t }^{ 2 } }$

Considering the following:

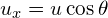${ u }_{ x }=u\cos\theta$ (horizontal vector of initial velocity, $u$ )
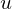${ a }_{ x }=0$ (horizontal velocity is constant)

We derive the following equation for the range:

$\Delta x={ { u }_{ x }t+\cfrac { 1 }{ 2 } \times 0\times { t }^{ 2 } }$

$\Delta x={ { u }_{ x }t$

Example 1:

A projectile is launched at 15 m/s at angle of 40° to the horizontal as shown below. It lands at the same height that it was launched. Calculate:

a) The maximum height

b) The time of flight

c) The range

Answers:

a) Using: ${ v }_{ y }^{ 2 }={ u }_{ y }^{ 2 }+2{ a }_{ y }\Delta y$

$0={ u }_{ y }^{ 2 }+2{ a }_{ y }\Delta y$

$0={ (u\sin\theta ) }^{ 2 }+2g\Delta y$

$\Delta y=\cfrac { -{ (u\sin\theta ) }^{ 2 } }{ 2g }$

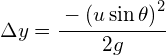
Where: (noting that down is positive)

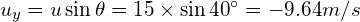${ u }_{ y }=u\sin { \theta } =15\times \sin { { 40 }^{ \circ } } =-9.64{ m }/{ s }$ (negative as initial vertical velocity is up)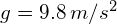
$g=9.8\:{ m }/{ { s }^{ 2 } }$

$\Delta y=\cfrac { -{ (-9.64) }^{ 2 } }{ 2\times 9.8 }$

$\Delta y=-4.74m$

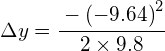
Therefore, maximum height reached = 4.74m

b) Using: ${ v }_{ y }=u_{ y }+a_{ y }t$ and ${ t }_{ total }\: =\: { 2t }_{ max\: height }$

$0=u_{ y }+gt$

$t=\cfrac { -u\sin { \theta } }{ g }$

Where: (noting that down is positive)

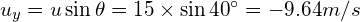${ u }_{ y }=u\sin { \theta } =15\times \sin {{ 40 }^{ \circ } } =-9.64{ m }/{ s }$ (negative as initial vertical velocity is up)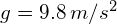
$g=9.8\:{ m }/{ { s }^{ 2 } }$

$t=\cfrac { -(-9.64) }{ 9.8 }$

$t=0.984$

Therefore, time of flight = $2\times 0.984=1.97$ seconds

c) Using $\Delta x={ { u }_{ x }t+\cfrac { 1 }{ 2 } { a }_{ x }{ t }^{ 2 } }$

Where:

${ u }_{ x }=u\cos \theta =15\cos {{ 40 }^{ \circ } } =11.49{ m }/{ s }$
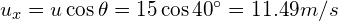
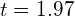$t=1.97$ (from part b)

$\Delta x={ { u }_{ x }t+\cfrac { 1 }{ 2 } \times 0\times { t }^{ 2 } }$

$\Delta x={ { u }_{ x }t$

$\Delta x=11.49\times 1.97=22.64m$