Energy in Orbits - Learn

Energy in Orbits – Learn

Total Energy of a Planet or Satellite in its Orbit

An orbiting satellite has two important forms of energy: gravitational potential energy, U, and kinetic energy, K. The sum of these two energies give us what is known as the total mechanical energy of the system, E. The equation for the total mechanical energy of an orbiting body is derived by combining the centripetal force of a satellite being equal to the force of gravity, with the magnitude of the force from Newton’s 2nd law and remembering the equation for the centripetal acceleration:

$F=\cfrac { GMm }{ { r }^{ 2 } } =\cfrac { { mv }^{ 2 } }{ r }$

$\therefore \: { mv }^{ 2 }\: =\: \cfrac { GMm }{ r }$

Incorporating the equation for kinetic energy by dividing by 2:

$\cfrac { 1 }{ 2 } { mv }^{ 2 }\: =\: \cfrac { GMm }{ 2r }$

And combining this with the equation for the gravitational potential energy of a satellite, the total energy is:

$E=K+U=\: \cfrac { GMm }{ 2r } -\cfrac { GMm }{ r } \:=\: -\cfrac { GMm }{ 2r }$

Therefore, total mechanical energy of a system:

$E \:=\: -\cfrac { GMm }{ 2r }$

Considering Kepler’s First Law

Remembering Kepler’s first law: The planets move in elliptical orbits with the Sun at one focus. This means that the distance between the centre of masses, r, will vary as a planet orbits the Sun. This results in a change in the gravitational potential energy of the planet as r varies.

Importantly, the total mechanical energy of the system remains constant throughout its orbit. As a planet orbits in a position that is close to the Sun, its gravitational potential energy will decrease, however, the planets velocity will increase and also its kinetic energy. The decrease in gravitational potential energy is balanced by the increase in kinetic energy so that the total mechanical energy of the system is always a constant. In summary:

Planets orbit the Sun in elliptical orbits
Total mechanical energy is always constant
As a planet orbits close to the Sun, the decrease in gravitational potential energy is balanced by the increase in kinetic energy
As a planet orbits further away from the Sun, the increase in gravitational potential energy is balanced by the decrease in kinetic energy

Energy Changes That Occur When Satellites Move Between Orbits

When a satellite changes its orbit there will be a change in its gravitational potential energy. This is given by the formula:

$\Delta U={ U }_{ f }\:-\:{ U }_{ i }$

Example 1:

A communications satellite orbiting the Earth at an altitude of 350km has a mass of 1250kg. The radius of the Earth, r_E = 6.4 × 10⁶ m and the mass of the Earth, m_E = 6.0 × 10²⁴ kg. Calculate:

a) The total mechanical energy of the satellite

b) The speed of the satellite

Answers:

a) Using: $E \:=\: -\cfrac { GMm }{ 2r }$

r = 6.4 × 10⁶ + 350000 = 6.75 × 10⁶ m (radius of orbit)

$E=-\cfrac { ({ 6.67\times 10 }^{ -11 })({ 6.0\times 10 }^{ 24 })(1250) }{ 2\times (6.75\times 10^{ 6 }) }$

$E\: =\: -3.71\times 10^{ 10 }\:J$

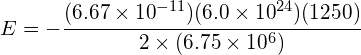
b) Using the equation for kinetic energy that had been derived:

$K=\cfrac { GMm }{ 2r }$

$K=\cfrac { ({ 6.67\times 10 }^{ -11 })({ 6.0\times 10 }^{ 24 })(1250) }{ 2\times (6.75\times 10^{ 6 }) }$

$K\: =\: 3.71\times 10^{ 10 }\: J$

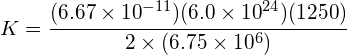
Using the equation for the kinetic energy: $KE\:=\cfrac { 1 }{ 2 } m{ v }^{ 2 }$

$\cfrac { 1 }{ 2 } m{ v }^{ 2 }\: =\: 3.71\times 10^{ 10 }\: J$

$1250{ v }^{ 2 }\: =\: 7.42\times 10^{ 10 }\: J$

${ v }^{ 2 }\: =\: 59360000$

${ v }\: =\: \sqrt { 59360000 }$

${ v }\: =\: 7704.54\: { m }/{ s }$

Example 2:

A meteor orbiting the Earth with an orbital radius of 8.2 × 10⁷ m moves to a lower orbit of 5 × 10⁷m. Calculate the change in gravitational potential energy if the meteor has a mass of 25kg. Mass of the Earth, m_E = 6.0 × 10²⁴ kg.

Answer:

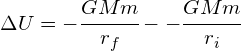
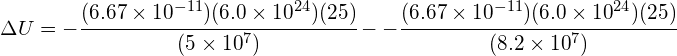
Using: $\Delta U={ U }_{ f }\:-\:{ U }_{ i }$

$\Delta U=-\cfrac { GMm }{ r_{ f } } --\cfrac { GMm }{ r_{ i } }$

$\Delta U=-\cfrac { (6.67\times 10^{ -11 })(6.0\times { 10 }^{ 24 })(25) }{ (5\times { 10 }^{ 7 }) } --\cfrac { (6.67\times 10^{ -11 })(6.0\times { 10 }^{ 24 })(25) }{ (8.2\times { 10 }^{ 7 }) }$

$\Delta U=-200100000+122012195$

$\Delta U=-7.81\times { 10 }^{ 7 }\:J$