Kepler’s Laws of Planetary Motion – Learn
Before Isaac Newton published his work on The Law of Universal Gravitation, which provided a concise theory to explain the orbits of the planets around the Sun, Johannes Kepler had proposed a theory based on the work he inherited from Tycho Brahe. Tycho Brahe had made meticulous measurements and observations of the Sun, planets and stars over many years and Kepler was able to use this data to propose a model for the motion of the planets (Tycho Brahe did all his work before the invention of the telescope). Whilst Kepler’s work was extensive, his theory is often summarised as three laws which although outdated by Newton’s work, are still of historical significance and interest.
Kepler’s Laws:
- First Law: The law of orbits
- Second Law: The law of areas
- Third Law: The law of periods
Kepler’s first Law: The law of orbits
Kepler’s first law states that all planets move in elliptical orbits with the sun at one focus and the other focus empty. The orbits of planets are almost circular and hard to distinguish on a scale diagram by eye.
Kepler’s second Law: The law of areas
Kepler noticed from his analysis of the data that the speed of the planets changed as they orbited the Sun and that a line from the Earth to the Sun would move through different angles in equal periods of time. From these observations, Kepler discovered that the further a planet was from the Sun, the slower it would be moving. Further to this he concluded for his second law, that a line joining the planet to the Sun would sweep through equal areas in equal periods of time.
Kepler’s third Law: The law of periods
Kepler was determined to find a relationship between the period of a planets orbit around the Sun and its average radius that was consistent for all planets. He eventually derived a relationship which is known as his third law: The cube of the average radius is proportional to the square of the orbital period of the planet.
This means that: ![]() is a constant for all planets.
is a constant for all planets.
Deriving from previous equations we find: 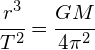
And: ![]() (planet 1) =
(planet 1) = ![]() (planet 2)
(planet 2)
Example 1:
Titan is a moon of Saturn. It has an orbital period of 15 days and 22 hours and an orbital radius of 1,200,000km. Calculate the mass of Saturn:
Answer: Need to convert r and T into SI units:
Orbital period, ![]()
Orbital radius, ![]()
Using: 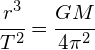
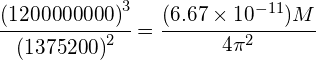
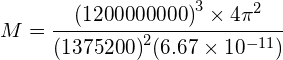
![]()
Example 2:
Mars has two moons: Phobos and Deimos. Phobos has an orbital period of 7.66 hours and an orbital radius of 9376 km. Calculate the orbital radius of Deimos if it has an orbital period of 30.35 hours:
Answer: Using: ![]() (planet 1) =
(planet 1) = ![]() (planet 2)*
(planet 2)*
*when using this relationship, the units for time and distance do not need to be in SI units. They must be in the same unit for each planet.
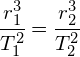
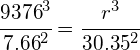
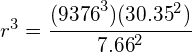
![]()
![]()
